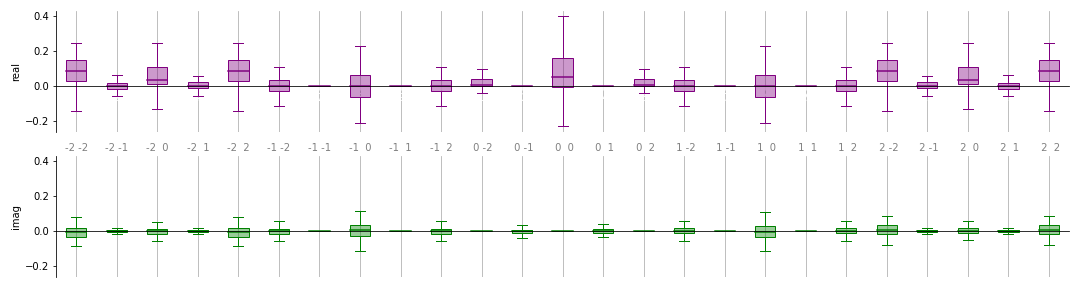
qml.fourier.visualize.box¶
-
box(coeffs, n_inputs, ax, colour_dict=None, show_freqs=True, show_fliers=True)[source]¶ Plot a list of sets of Fourier coefficients as a box plot.
- Parameters
coeffs (list[array[complex]]) – A list of sets of Fourier coefficients. The shape of the coefficient arrays should resemble that of the output of numpy/scipy’s
fftnfunction, orcoefficients().n_inputs (int) – The number of input variables in the function.
ax (array[matplotlib.axes.Axes]) – Axis on which to plot. Must be a pair of axes from a subplot where
sharex="row"andsharey="col".colour_dict (dict[str, str]) – A dictionary of the form {“real” : colour_string, “imag” : other_colour_string} indicating which colours should be used in the plot.
show_freqs (bool) – Whether or not to print the frequency labels on the plot axis.
show_fliers (bool) – Whether to display the box plot outliers.
- Returns
The axes after plotting is complete.
- Return type
array[matplotlib.axes.Axes]
Example
Suppose we have the following quantum function:
dev = qml.device('default.qubit', wires=2) @qml.qnode(dev) def circuit_with_weights(w, x): qml.RX(x[0], wires=0) qml.RY(x[1], wires=1) qml.CNOT(wires=[1, 0]) qml.Rot(*w[0], wires=0) qml.Rot(*w[1], wires=1) qml.CNOT(wires=[1, 0]) qml.RX(x[0], wires=0) qml.RY(x[1], wires=1) qml.CNOT(wires=[1, 0]) return qml.expval(qml.Z(0))
We would like to compute and plot the distribution of Fourier coefficients for many random values of the weights
w. First, we generate all the coefficients:from functools import partial coeffs = [] n_inputs = 2 degree = 2 for _ in range(100): weights = np.random.normal(0, 1, size=(2, 3)) c = coefficients(partial(circuit_with_weights, weights), n_inputs, degree) coeffs.append(c)
We can now plot by setting up a pair of
matplotlibaxes and passing them to the plotting function:>>> import matplotlib.pyplot as plt >>> from pennylane.fourier.visualize import box >>> fig, ax = plt.subplots(2, 1, sharey=True, figsize=(15, 4)) >>> box(coeffs, n_inputs, ax, show_freqs=True)